Heap Sort Java Program

This tutorial shows how to write Heap sort program in Java which is an in-place sorting algorithm. Heap sort uses heap data structure for sorting the elements so the obvious question is what is heap?

Table of contents

Heap data structure
Heap sort algorithm
How to create heap from array
Heap Sort Java program
Heap sort time and space complexity

Heap data structure

A heap is a binary tree so each node can have maximum two children and it has following properties-

It is a complete binary tree which means reading from left to right it is completely filled in (all the nodes have 2 children) except the last row which need not be full.
Each node in the heap satisfies the condition that each node is greater than or equal to its child nodes in case of Max heap. Node is less than or equal to its child nodes in case of Min heap.

Heap sort algorithm

Steps for writing the Heap Sort Java program are as follows-

Create a max heap from input array. Using max heap sorting will be done in ascending order. For descending order you can use min heap. Heap data structure is also represented using array. This process of creating heap from the input array is called heapify.
Once the heap is created its root node is the maximum element. Swap the root element with the last element of the array.
This swapping disturbs the heap so structure has to be heapified again using the array. This time last element is excluded (array length decreased by one) as it is already at its final place.
Repeat step 2 and 3 until sorting is complete.

How to create heap from array

Creating heap from an array is an important part of heap sort so understanding it is important.

Array is considered as a complete binary tree with each element considered as a node. With in an array for each node you can get its parent node, left child node and right child node using the following equations-

For a node at index i in the array-

Parent node is– (i-1)/2
Left child node is- 2*i + 1
Right child node is- 2*i+2

To create a heap you'll have to start from the nodes at the bottom and move upwards comparing if child node is greater than the parent and swapping node values if that is true. Since last level has leaf nodes (nodes with no children) so this comparison has to be started from one level above.

For an array of length n, last node will be at index (n-1) thus the index of its parent node should be (n-1)/2 using the equation. Heapifying the array starts from this parent node, in each iteration compare the parent node with left child and right child and swap the nodes if child is greater than the parent.

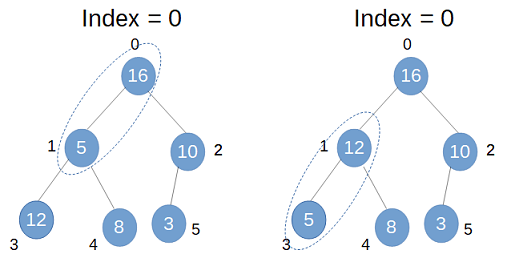
For example if input array is [5, 12, 3, 16, 8, 10] then the complete binary tree for this array can be visually represented as-

Since last index is 5 thus the parent node should be at index (5-1)/2 = 2. Process of creating a heap starts from that index 2. Compare node at index 2 with its child nodes and swap if any of the child is greater than the parent node. In our tree 10 > 3 so these values are swapped. When index is 1, node at index 1 is compared with its child nodes and values swapped if required.

In next iteration comparison and swapping is done for index 0.

Heap Sort Java program

public class HeapSort {

  public static void main(String[] args) {
    int[] arr = {5, 12, 3, 16, 8, 10};	
    System.out.println("Original array- " + Arrays.toString(arr));
    HeapSort hs = new HeapSort();
    hs.heapSort(arr);
    System.out.println("Sorted array after heap sort- " + Arrays.toString(arr));
  }
	
  private void heapSort(int[] arr){
    int arrLength = arr.length;
    // create heap from array start from index (n-1)/2
    for(int i = (arrLength-1)/2; i >= 0; i--){
      heapify(arr, arrLength, i);
    }
    System.out.println("heapified array- " + Arrays.toString(arr));
    // Heap Sort 
    for(int i = arrLength-1; i >= 0; i--){
      // Swap root and last nodes 
      swap(arr, i, 0);
      // Reconstruct heap again 
      heapify(arr, i, 0);
    }
  }
    
  private void heapify(int[] numArr, int index, int i){
    // Getting parent and children indexes
    int root = i;
    int leftChild = 2*i + 1;
    int righChild = 2*i + 2;
    //compare left child value
    if(leftChild < index && numArr[leftChild] > numArr[root])
      root = leftChild;
    //comparing right child value
    if(righChild < index && numArr[righChild] > numArr[root])
      root = righChild;
      // swap values if required and call method recursively for next level
      if(root != i){
        swap(numArr, root, i);
        heapify(numArr, index, root);
      }
    }
    
    private void swap(int[] numArr, int index, int li){
      int temp = numArr[li];
      numArr[li] = numArr[index];
      numArr[index] = temp;
    }
}

Heap sort time and space complexity

Time required to do any common tree operation is O(logn). For Heap sort creation of heap is done for n elements thus the time complexity of Heap sort is O(n*logn). This time complexity remains the same however the data is distributed. That’s where Heap sort scores over Quick sort which is another O(n*logn) sorting algorithm. In worst case Quick sort may become O(n2) but Heap sort is always O(n*logn).

Since same array is used for arranging the elements in order so no extra space requirement is there. Thus the space complexity of Heap sort is O(1).

That's all for the topic Heap Sort Java Program. If something is missing or you have something to share about the topic please write a comment.

You may also like

KnpCode

January 28, 2023